Today I'm going to reveal a classified archive. Or so it seems...
Physicians have been keeping this knowledge from us simple mortals for centuries...hehehe...
While trying to understand the essentials on variational mechanics, I have come into this article: http://jazz.openfun.org/wiki/Brachistochrone.
The problem of the brachistochrone dates back to Newton (17th century) and appears mentioned frequently as one of the problems that can be solved be means of this refined technique.
In fact, this problem appears to be the actual trigger for the modern physics (or better stated, its solution), and reveals a completely counterintuitive phenomenon:
The quickest path is not the straight line
Amazingly, the solution for a bead on a wire going in the least time from point A to point B:
Is the cycloid represented in the picture.
As standard human, one always tends to think that the shortest path would be the quickest one. It is wrong.
Analogously, when it comes to minimize the action (see previous posts on the subject), it is very hard to imagine that the stationary points would not come at flattening the curve for the action.
This is what makes so hard to understand the variational principles that rule over Lagrangian, Eulerian and Hamiltonian mechanics.
If one only had been told...
I have made a spreadsheet with openoffice (www.openoffice.org) where this can be numerically perceived also.
The spreadsheet is here.
I have made it with the help of a paper by Jozef Hanc: The original Euler's calculus-of-variations method: Key to Lagrangian mechanics for beginners.
I found it extremely appropriate for my case, and also absolutely clarifying. Thanks mr Hanc
This is the blog-diary created to monitorize the evolution of Rabindranath Andujar's thesis on Stochastic Simulation and Lagrangian dynamics applied to Structural Design. It is intended to extend collaboration with other people, allow the register of the studies, and force a discipline on recording references, lines of study, and whatever else appears.
miércoles, 31 de marzo de 2010
domingo, 28 de marzo de 2010
Ilustrating Lagrangian Variables
In the last post we had a tentative on Variational Mechanics which resulted very stimulating.
In order settle ideas down, I have left the subject cooling in the fridge and I have fiddled around with the Lego Mindstorms(c) robot we have at the RGEX research group, trying to make a positioning system that is accurate enough for our purposes.
Surely Jaume (my thesis director) will be very happy to hear about it.
I know this is not the exact place for it, but it's my blog and I do what I want to...hehehe...anyway, whoever wants to see what we do there, it is available at: www.rgex.blogspot.com.
And now, back to work:
The intention of this post it to illustrate some relationships that exist in Mechanics and that are repeated ad-vomitum in every reference one finds on Variational Mechanics.
The main problem I have encountered is that explanations mix numerical methods with physical concepts, and more often that seldom everything is written in the cryptic language of mathematicians. Of course, in complete absence of figures or anything of the like.
So, here we go...
With the help of some coding in C++ and QtOctave (https://forja.rediris.es/projects/csl-qtoctave/), I have made some graphics for the simulation of a moving particle.
I have used the same deductive principle I have seen in the papers, which is not intuitive at all. Hopefully some drawings will make it more clear.
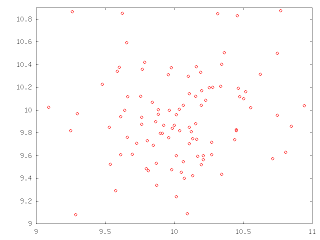
A moving particle
Instead of trying to obtain the formula in a straightforward manner, the Least Action Principle suggest one to imagine an arbitrary particle that changes its position from one place to another. So, that's exactly what I have done.
The code iterates some 100 times and assigns random values to the new position of our particle. Really simple stuff.
The red dots represent all 100 different positions the particle goes when random increments in x and y are applied.
The initial point is at (10,10), and all the following are dQ further (dQ is divided in X and Y components, of course). dQ gets a random value for each iteration.
Once we have the new positions, it is straightforward to apply physics concepts to get the values of Velocity, Acceleration, Kinetic Energy and Potential Energy that have to be applied to get the particle there:
With a dt value of 0.1 and a mass m of 5, it is also a piece of cake to obtain a table with the respective values.
Work and energy
The magnitudes Work and Energy are directly related to the Ep and Ec values.
From a physical point of view, there are some very interesting things that can be observed when putting their values against the |dQ| values:
The basic variational principle
The following step once these observations are made, is that of nesting our little freely moving particle loop into another broader loop, and accumulate the values of the position to form a trajectory.
Provided the inner loop generates a bunch of 100 probable future positions, one tempting criterion would be to choose that of minimum value for the total calculated energy...
main.cpp:
In order settle ideas down, I have left the subject cooling in the fridge and I have fiddled around with the Lego Mindstorms(c) robot we have at the RGEX research group, trying to make a positioning system that is accurate enough for our purposes.
Surely Jaume (my thesis director) will be very happy to hear about it.
I know this is not the exact place for it, but it's my blog and I do what I want to...hehehe...anyway, whoever wants to see what we do there, it is available at: www.rgex.blogspot.com.
And now, back to work:
The intention of this post it to illustrate some relationships that exist in Mechanics and that are repeated ad-vomitum in every reference one finds on Variational Mechanics.
The main problem I have encountered is that explanations mix numerical methods with physical concepts, and more often that seldom everything is written in the cryptic language of mathematicians. Of course, in complete absence of figures or anything of the like.
So, here we go...
With the help of some coding in C++ and QtOctave (https://forja.rediris.es/projects/csl-qtoctave/), I have made some graphics for the simulation of a moving particle.
I have used the same deductive principle I have seen in the papers, which is not intuitive at all. Hopefully some drawings will make it more clear.
A moving particle
Instead of trying to obtain the formula in a straightforward manner, the Least Action Principle suggest one to imagine an arbitrary particle that changes its position from one place to another. So, that's exactly what I have done.
The code iterates some 100 times and assigns random values to the new position of our particle. Really simple stuff.
The red dots represent all 100 different positions the particle goes when random increments in x and y are applied.
The initial point is at (10,10), and all the following are dQ further (dQ is divided in X and Y components, of course). dQ gets a random value for each iteration.
Once we have the new positions, it is straightforward to apply physics concepts to get the values of Velocity, Acceleration, Kinetic Energy and Potential Energy that have to be applied to get the particle there:
V=dQ/dt
A=dV/dt
Ep=m*A*dQ
Ec=1/2(m*|V|²)
With a dt value of 0.1 and a mass m of 5, it is also a piece of cake to obtain a table with the respective values.
Work and energy
The magnitudes Work and Energy are directly related to the Ep and Ec values.
From a physical point of view, there are some very interesting things that can be observed when putting their values against the |dQ| values:
Distance |dQ| vs kynetic energy Ec
Distance |dQ| vs potential energy Ep
From the same experiment, the random values of distance show a correlation of two types with the respective energies:
- Kynetic energy is linearly related to the distance covered by the particle. Its values depend solely on the module of the velocity parameter, which itself is linearly dependent on the distance.
- Potential energy shows a more quadratic behaviour, provided its acceleration component is multiplied by the covered distance.
Kynetic energy Ec vs Potential energy Ep
Interestingly enough, both (|dQ| vs Ep) and (Ec vs Ep) are exactly the same shape, but for the scale of the X axis, which is of course linearly related.
The basic variational principle
The following step once these observations are made, is that of nesting our little freely moving particle loop into another broader loop, and accumulate the values of the position to form a trajectory.
The random accumulated trajectory of the particle
Just to verify that by adding the minimum energy substeps we still get a random trajectory.
Obviously, no constraints have been applied, and the particle represents a "Markov process".
What the basic variational principle teachs us is that, given certain constraints, the trajectory of the particle would have been that of minimum energy.
In our code for each time step the chosen subpath has been that of minimum energy.
Nonetheless, for the global trajectory, i.e. after a series of timesteps, a more holistic approach has to be taken in order to obtain the actual "natural" path.
That is the ODEs approach, and we'll talk about it in further episodes...
The following is the C++ code employed to obtain the tables. These have been plotted with QTOctave, an opensource version of MathLab.
Please note that it is the version which provides the complete path. The inner loop provides the random new positions and the outer loops concatenates one position after another, selecting each time that with the minimum energy.
Nonetheless, for the global trajectory, i.e. after a series of timesteps, a more holistic approach has to be taken in order to obtain the actual "natural" path.
That is the ODEs approach, and we'll talk about it in further episodes...
The following is the C++ code employed to obtain the tables. These have been plotted with QTOctave, an opensource version of MathLab.
Please note that it is the version which provides the complete path. The inner loop provides the random new positions and the outer loops concatenates one position after another, selecting each time that with the minimum energy.
main.cpp:
sábado, 20 de marzo de 2010
ACTION!
One more week spent on Lagrangian Dynamics...and more results!
Well, the main point about Lagrange and his ubiqutous formulae (that following level of abstraction I talked about in the last post), passes through the concept of ACTION.
Inexplicably, when learning physics at the Secondary or even at the Graduate studies, everything seems to finish when we get to the three laws of Newton.
That's the highest point one ever gets...and then we reach the concept of energy by integrating forces along paths.
But there is still one step further (or maybe more, now that the world seems to be round instead of flat, one never knows...).
The notion of action is that of the integral of the energy along time. Easy, isn't it? Its units are energy·time (Joule-second in SI).
Ok then. The problem, I guess, is that in order to be able to do something useful with it, one has to go also one step further in the mathematical notion of function: that of Functional.
And perhaps here is where our poor brains become at risk of melting...or maybe not, because a functional is just a function where the variable is...a function.
So, we are supposed to understand and memorize the linearity property of the integrals, and not the idea of functional? Come on...
Anyway, let's forgive our poor teachers of calculus and physics, who did their best I am sure, and get to work...
The discipline in charge to explain functionals is Variational Calculus, a fairly complex matter. When applied to physics, it happens to produce the Variational Principle of Physics, which is on where all Lagrangian, Jacobian, Hamiltonian and Eulerian dynamics rest.
So , in order to properly grasp the ideas of Lagrangian Dynamics, we better start with a little revision. The best one I found is from Mr. Claude Lacoursière's thesis "Ghost and machines: Regularized Variational Method for Interactive Simulation Multibodyes with dry friction" , combined with the following extremely clear explanation of the concept of action (http://wapedia.mobi/en/Action_(physics)):
1.-Work and Energy:
When a force is applied over a mass along a trajectory kinetic energy is dissipated. Integrating the formula, we can obtain its value as:
T(x')=(m·||x'||²)/2
where x' (aka velocity) is the derivative of the position, m is the mass of the particle and T(x') is the total kinetic energy.
For the cases when the force assumes values tangent to the energy function, then another form of energy appears: this is potential energy.
This special form of energy has the special property of being independent of the trajectory.

And this form of energy must also be considered into our energy equation if we want to account for everything.
This leaves our equation for the energy of the system the following way:
E=T(x')+V(x)
Being T(x') the kinetic energy described above and V(x) the potential energy.
2.-Basic Variational principle:
This would be, as explained above, the integral of this equation over time.
Here, t1 and t2 are the initial and final time positions, and L(x,x') is our LAGRANGIAN, which is exactly our Energy Equation, but with another name.
The funny thing about this integral is that it solves nothing by itself. There is a lot of possible solutions for our trajectory, all of them valid in mathematical terms, but only one of them is good for us.

The D'Alembert principle states that, "for a physical trajectory and infinitesimal displacements thereof at each point in time, and compatible with all imposed constraints, the work done by the virtual displacements along the trajectory vanishes when the motion is not bounded, and non-positive otherwise".
In plain English: the path followed is going to be that for which the action is minimized (or more strictly, for which the action is stationary, i.e. there is a minimum point).
∂L/∂xi - d/dt ( ∂L/∂xi' ) = 0
And then use the mathematical technique of the Lagrangian Multipliers (which I will not explain here), in order to simplify our Action Integral into something we can operate with, i.e. a second order differential equation.
And this is it. The basis, the cornerstone of Lagrangian Dynamics, demystified.
Once these concepts are comprehended, it is relatively easy to toddle around all the rest of this vast world...now at least we have legs!
domingo, 14 de marzo de 2010
LAGRANGIAN DYNAMICS
These days I've been researching on Lagrangian Dynamics.
Finally, some light has been shed through the thick mesh of formulae, technical and mathematical verbiage, and an atom of understanding has entered into my banged head.
The paper that has finally put everything together is this:
http://box2d.googlecode.com/files/GDC2009_ErinCatto.zip
But before, I have had to go through an odissey of other papers to understand why they call it Lagrangian Dynamics, and Lagrangian by extension, to everything related to dynamics in the latest physics simulation R+D world.
The thing is as follows, explained in plane English for plane human beings (like myself, ahem...):
Classical Newtonian mechanics have some limitations when it comes to computing the equations of motion.
We want to iteratively solve a set of Ordinary Differential Equations (ODE) for acceleration, velocity and position if we want to know where our physical elements will be.
But it happened that mysteriously, when computing them, the total energy of the system got affected, because dissipative forces like damping, friction, etc... had to be also implemented, at that is a daunting task...
And there is where Lagrange comes into play: he theorized that we can make use of a further abstraction of our system and embed it into another, a bit broader conceptually, where all these forces would not be so determinant and we still could retrieve our results for position, by applying energetic conservation concepts.
Of course this abstraction comes at the price of having to understand a lot of many other things, not simple either (one funny thing about all this is that the only examples I have been able to find are that of a pendulum, a spring tied to a mass and a bead on a wire...If you didn't get it at the beginning, you'll never do...until you get it. Then these are so obvious you can't think of another!)
Anyway, the main point on Lagrangian approach to dynamics is that we can (and we normally do) find a set of equations that constraint the movement so the energy of the particles individually remains untouched.
These constraints materialize in the form of Jacobian Matrices or Lagrange Multipliers applied to each particle, rigid body or mass in a mass-spring system into our simulation (this is much deeper explained in the paper).
Fortunatelly also, all the above can be applied to Finite Element Method meshes. All we have to consider is that, in Lagrangian dynamical FEM, instead of having only one term for the stiffness matrix as usual:
[F]=[K]·[u]
a few more matrices that represent the dynamic terms appear:
[M][u''] + [C][u'] + [K][u] = [F]
And this is it regarding brand new concepts. It is as far as I can go by now.
In the way I have encountered many intensely related diverse topics, which should be explained in following posts. Some of them are:
Finally, some light has been shed through the thick mesh of formulae, technical and mathematical verbiage, and an atom of understanding has entered into my banged head.
The paper that has finally put everything together is this:
http://box2d.googlecode.com/files/GDC2009_ErinCatto.zip
But before, I have had to go through an odissey of other papers to understand why they call it Lagrangian Dynamics, and Lagrangian by extension, to everything related to dynamics in the latest physics simulation R+D world.
The thing is as follows, explained in plane English for plane human beings (like myself, ahem...):
Classical Newtonian mechanics have some limitations when it comes to computing the equations of motion.
We want to iteratively solve a set of Ordinary Differential Equations (ODE) for acceleration, velocity and position if we want to know where our physical elements will be.
But it happened that mysteriously, when computing them, the total energy of the system got affected, because dissipative forces like damping, friction, etc... had to be also implemented, at that is a daunting task...
And there is where Lagrange comes into play: he theorized that we can make use of a further abstraction of our system and embed it into another, a bit broader conceptually, where all these forces would not be so determinant and we still could retrieve our results for position, by applying energetic conservation concepts.
Of course this abstraction comes at the price of having to understand a lot of many other things, not simple either (one funny thing about all this is that the only examples I have been able to find are that of a pendulum, a spring tied to a mass and a bead on a wire...If you didn't get it at the beginning, you'll never do...until you get it. Then these are so obvious you can't think of another!)
Anyway, the main point on Lagrangian approach to dynamics is that we can (and we normally do) find a set of equations that constraint the movement so the energy of the particles individually remains untouched.
These constraints materialize in the form of Jacobian Matrices or Lagrange Multipliers applied to each particle, rigid body or mass in a mass-spring system into our simulation (this is much deeper explained in the paper).
Fortunatelly also, all the above can be applied to Finite Element Method meshes. All we have to consider is that, in Lagrangian dynamical FEM, instead of having only one term for the stiffness matrix as usual:
[F]=[K]·[u]
a few more matrices that represent the dynamic terms appear:
[M][u''] + [C][u'] + [K][u] = [F]
And this is it regarding brand new concepts. It is as far as I can go by now.
In the way I have encountered many intensely related diverse topics, which should be explained in following posts. Some of them are:
- Linear Complementary Problem Solvers
- Principle of Virtual Work
- Differential Equations
- Smoothed Particle Hydrodynamics (SPH)
- Kynematics
miércoles, 10 de marzo de 2010
Stiffness Method and SBRA
Eventually I have managed to implement the full code for a simple Direct Stiffness calculator.
The previous post has been conveniently modified to reflect this.
The results have been fairly discouraging for my intemptions to use it as a basis for the SBRA: initial research led me to the wrong idea that the most computationally intensive part was that of assembly of the stiffness matrix, but my own experiments have proven the opposite.
The code provided, on a 1.66 GHz processor (the computer is actually dual core, but no parallelization was used), with 2GB RAM, takes 46 seconds only in the solving part. The modelled structure is 1000 nodes and 1800 elements large.
According to the paper, about 10⁷ iterations are needed over the solver to get a proper reliability assessment. Hence, grosso modo, applying SBRA to this structure on this computer would take 46*10⁷ seconds, some 14.5 long years.
It is likely that, for smaller structures and using parallelization, times become significantly smaller.
Nonetheless, the point I wanted to make here is that of the solving step being the most computationally intensive, instead of the presumed assembly step.
The previous post has been conveniently modified to reflect this.
The results have been fairly discouraging for my intemptions to use it as a basis for the SBRA: initial research led me to the wrong idea that the most computationally intensive part was that of assembly of the stiffness matrix, but my own experiments have proven the opposite.
The code provided, on a 1.66 GHz processor (the computer is actually dual core, but no parallelization was used), with 2GB RAM, takes 46 seconds only in the solving part. The modelled structure is 1000 nodes and 1800 elements large.
According to the paper, about 10⁷ iterations are needed over the solver to get a proper reliability assessment. Hence, grosso modo, applying SBRA to this structure on this computer would take 46*10⁷ seconds, some 14.5 long years.
It is likely that, for smaller structures and using parallelization, times become significantly smaller.
Nonetheless, the point I wanted to make here is that of the solving step being the most computationally intensive, instead of the presumed assembly step.
viernes, 5 de marzo de 2010
DSF Implementation
Well...the following is the C++ code to achieve the initial stages of the DSF (e.g. member formation, globalization, merging and linear solving):
main.cpp:
Element.h:
Element.cpp:
Node.h:
Node.cpp:
Stiffness.h:
Stiffness.cpp:
I have used the GSL library for everything related to maths (http://www.gnu.org/software/gsl/).
This will make my life a lot easier once I manage to master it...Is fairly well documented, so it won't take long (I hope).
Please note that to make the timer work, under Ubuntu 9.10, I've had to activate the -lrt tag in the linker.
main.cpp:
Element.h:
Element.cpp:
Node.h:
Node.cpp:
Stiffness.h:
Stiffness.cpp:
I have used the GSL library for everything related to maths (http://www.gnu.org/software/gsl/).
This will make my life a lot easier once I manage to master it...Is fairly well documented, so it won't take long (I hope).
Please note that to make the timer work, under Ubuntu 9.10, I've had to activate the -lrt tag in the linker.
miércoles, 3 de marzo de 2010
Direct Stiffness Method
Well...as promised, these past days I've been researching on the possiblity of efficiently use the SBRA through the application of MonteCarlo methods.
I have been successful in my research and I have found this very interesting course:
http://www.colorado.edu/engineering/cas/courses.d/IFEM.d/
It is extremely complete!!
I have used it to refresh my rusted matrix knowledge from my university years, and so far I have managed to implement a very simple program - though effective for my purposes - that will allow me to benchmark the most time-consuming tasks in classical analysis.
This is a very brief resume of the algorithm from the course outlined above:
DIRECT STIFFNESS METHOD STEPS
I will provide the lines of code in the following posts.
I have been successful in my research and I have found this very interesting course:
http://www.colorado.edu/engineering/cas/courses.d/IFEM.d/
It is extremely complete!!
I have used it to refresh my rusted matrix knowledge from my university years, and so far I have managed to implement a very simple program - though effective for my purposes - that will allow me to benchmark the most time-consuming tasks in classical analysis.
This is a very brief resume of the algorithm from the course outlined above:
DIRECT STIFFNESS METHOD STEPS
- Breakdown
- Disconnection
- Localization
- Member Formation
- Assembly
- Globalization
- Merge
- Application of boundary conditions
- Solution
- Recovery of derived quantities
I will provide the lines of code in the following posts.
Suscribirse a:
Entradas (Atom)